| Introduction | >>Models<< | Simulator | Results | References |
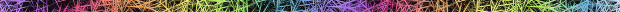
The goal of these models is to determine how spiral patterns evolve in the aggregation stage of Dictyostelium development. Since most of the qualitative features of the spiral waves can be explained solely by considering a slime mold colony as an excitable medium, much of the complications of the intracellular cAMP signalling system elements are ignored.
Described in KL93, the first model models slime mold cells as simple automata they call "bions". Bions have three states. In state 0 a bion is excitable, and a local cAMP concentration greater than a fixed threshold causes the bion to become excited (state 1). In state 1 bions emit a certain amount of cAMP over several time units. After that time a bion enters state 2, the refractory state, where it is not excitable. It remains in state 2 for a fixed number of time units and then re-enters state 0.
The model places bions randomly with a certain density in a two-dimensional grid. The cAMP concentration c is assumed to obey the equation
where a² is the normalized diffusion constant, gamma is the degradation constant due to phosphodiesterase (which is assumed to be at a constant uniform concentration), and the sources are those slime mold cells that are releasing cAMP.
The paper does not describe in detail the initial conditions for their simulations. Most likely some cell(s) are chosen randomly to fire (release cAMP) to generate initial waves, but after waves are propagating no cells randomly fire. The paper shows one result of their simulations, a spiral that formed on a 100x100 grid:

Presumably it took many simulation runs and tweaking of the initial conditions to yield this result, since LATT96 claims that some dynamically varying element is needed in order for spirals to form consistently with random initial conditions, as explained below.
The second model is described in LATT96. It is based on the first model. Random firing is modeled by having a cell that has not fired for 15 time steps fire. The paper first shows that without unrealistic initial inhomogeneities, spiral waves do not form. Instead the initial random firings lead to concentric waves that die out and are restarted when more random firings occur, as shown in the following picture from the paper:

The second model adds variable excitability to cells in the form of variable cAMP firing thresholds. It also adds a relative refractory period in between the absolute refractory period and the excitable state. During the relative refractory period the firing threshold decreases from a maximum value to the excitable level.
A cell's excitability is modeled as a dynamic variable E. E affects the firing threshold (the firing threshold is multiplied by (1-E)), and E increases as more cAMP binds to a cell, up to a maximum value. This models the increased excitability seen in real slime mold cells due to gene expression increases as the aggregation process progresses. E follows this equation:
where the decrease is due to degradation of signalling pathway components and the increase is proportional to the concentration of cAMP.
When every cell's excitability increases uniformly as the aggregation continues, small patterns form but no global patterns form (the top row of images in the following picture, with time increasing from left to right). Global patterns are large-scale patterns with only a few aggregation centers. Only when the excitability increases with individual cAMP binding and cells have variable firing thresholds do global spiral patterns emerge (bottom row of images).

FL98 models several genetic elements in the cAMP signalling pathways. Their cells progress from excitable to self-oscillatory to excitable again, excitability increasing with time. Self-oscillatory regions generate rings which break and develop into spirals, which then take over the wavefield.
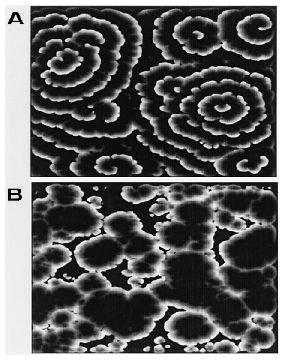
They claim that variable excitability explains several phenomena. Spirals do not form at low cell density because the system never gets excitable enough. Also, wave resetting experiments have been performed where cAMP is sprayed on a slime mold colony during aggregation. When cAMP is added early in the aggregation stage, spiral waves reappear (A in the picture below). When cAMP is added later when spirals are large and well-formed, spirals do not reappear (B in the picture below). Genetic feedback explains these results: the added cAMP in the second experiment causes all cells to reach the maximum level of excitability, and the lack of variable excitability prevents spirals from reforming, while in the first experiment the cells advance in excitability but are not far enough in the aggregation process to reach the maximum.
| Introduction | >>Models<< | Simulator | Results | References |