


| Introduction | Models | Simulator | >>Results<< | References |
Spiral patterns form occasionally if the random initial arrangement and cell chosen to fire are such that the circular wave leaving the firer breaks on one side and by the time the other sides curl around, the cells in the center (around the initial firer) are once again excitable. Here are some patterns obtained when simulating the first model:



You can also view an animation (1.6MB) of the second picture above.
These results are consistent with KL93. The paper does not say how frequently spirals were achieved, nor what the initial conditions are.
This is essentially the same setup as the first model, but with different initial conditions. Instead of a few cells randomly firing initially and again when there is no activity in the system for a while, each cell fires if it is not excited in a certain amount of time (it has a probability of firing that is tested at each time step beyond 14 of no excitation). This leads to multiple outgoing circular waves. Even if one breaks on one side the others quickly fill in that side, making it less likely for a spiral to form. In all my runs I never saw anything but the circles expanding, annihilating where they hit each other, and diffusing off the edge. This is exactly what LATT96 describes, bursts that die out. Note that if initial conditions more like the first model are used here, spirals can and do form. Such initial conditions are less realistic, however.

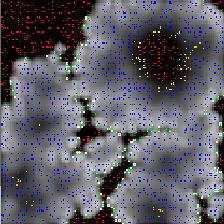
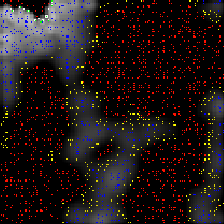
The above pictures are of the same simulation with time increasing from left to right. You can view an animation (400KB) of the simulation.
I had several problems duplicating the parameters of the second model with variable excitability. LATT96 is not entirely clear on whether the cAMP threshold for bions in the excitable state should also be multiplied by (1-excitability) just as it is in the relatively refractory state; I assume that it is. Also, the given degradation constant (gamma) and excitability increase constant (beta) are both orders of magnitude higher than I believe they should be. If beta is not less than 0.01 or even lower, the excitability increases much too quickly.
I tried modifying the unknown parameters in many ways, and the only way I can duplicate the paper's results are by initializing all cells' time since last firing to 0 and having a less than 1 probability of each cell firing at each time step beyond 15 since last firing. This leads to most cells firing at the same time, beginning on global time step 15. The cells that do not fire at that time then have a number of time steps to spread their waves, which collide with the next mass firing and stop it in its tracks. This continues until those "rebel" cells become centers in large waves that reach a limit cycle. A typical result is shown in picture on the left below. Also, an animation (1MB) of this process can be viewed.
With the much more realistic setting of each cell starting out with a random time since last firing, so that they do not all fire at once, the system begins promisingly. Lev98 describes the beginning as "initial bursts die out, but leave a memory of their propagation paths in the form of a variable excitability." The simulator's coloring shows this happening. What should happen for spiral waves to form is that local waves begin to break on less-excitable areas of the grid and form spirals, which eventually destroy competing spirals and lead to global patterns. However, no matter what the excitability increase and decrease constants are set to, by the time the excitabilities of the cells are high enough for local spirals to form, cells everywhere have moderately high excitabilities and the spirals cannot destroy each other. The system often reaches a limit cycle (since nondeterminism vanishes once waves are all over the grid, preventing random firings), and even when run for long amounts of time makes no progress towards global patterns. The results look like the middle picture below, and this animation (1.1MB).
By increasing the diffusion to unrealistic levels, more global patterns are created. This can be seen in the right-hand picture below and in this animation (600KB).



The first model's results were simple to duplicate. The second model's parameters and initial conditions had to be modified to mesh with my understanding of the situation. A misunderstanding of some kind probably led to my inability to duplicate the second model's results without using unrealistic parameters.
These models can be made more realistic by including chemotaxis, non-uniform degradation, and self-oscillatory cells.
Both the first and second models ignore chemotaxis during aggregation. They both turned it on at later stages to watch cell streaming and mound formation. This begs the question of what effect chemotactic movement has on the early stages of these models.
Both models assume non-uniform degradation. The phosphodiesterase secreted by cells apparently increases as aggregation continues, making this assumption unrealistic.
In some strains of Dictyostelium concentric ring waves appear. These are due to autonomous periodic signalling by cells in the center of the rings (spiral waves do not require autonomous oscillations because the rotating spiral excites itself). In principle, nearly every cell can become self-oscillatory. Cells progress during aggregation from being non-excitable to being excitable to being self-oscillatory [Wei99]. The third model considers cells that are a certain way along its excitability development timeline to be self-oscillatory, but the other models ignore self-oscillations. It would be interesting to see what happens when randomly selected cells become self-oscillatory in the simplest model, the first model, and also in both models at low density. According to LATT96, at low density aggregation only progresses with formation of concentric ring waves due to self-oscillatory cells.
| Introduction | Models | Simulator | >>Results<< | References |